07.3 Kohlenstoff- und Stickstoffumsatz im Boden

Der Umsatz zwischen den einzelnen C/N-Bindungsformen (Abb. 7‑2) wird durch eine Kinetik erster Ordnung beschrieben (Chertov and Komarov, 1997; Franko, 1990; Parton et al., 1987). Die Umsatzgeschwindigkeit wird durch reaktionsspezifische Umsatzkoeffizienten bestimmt.

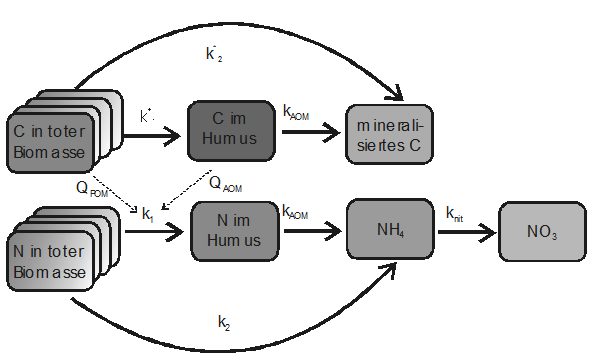
Abb. 7‑2: Modell des Kohlenstoff-Stickstoff-Umsatzes mit den Reaktionskoeffizienten k₁+k₂ = k*₁+k*₂ = k_POM für die Primärsubstanz, k_AOM für die aktive organische Substanz, den entsprechenden C/N-Verhältnissen Q_POM bzw. Q_AOM und der Nitrifikationskonstante k_nit

Der dominante Prozess ist die C-Mineralisierung, welcher die Energie für den gesamten Umsatz der organischen Substanz liefert. Entsprechend des obigen Konzeptes ergibt sich die Änderung der Kohlenstoffmenge in der organischen Primärsubstanz POM wie folgt:

(56)

mit dem Reaktionskoeffizienten k_POM = k*₁+k*₂ (s. Abb. 7‑2). Die Reduktionsfunktion R_min repräsentiert den Einfluss von Wassergehalt, Bodentemperatur und pH-Wert auf den Mineralisierungsprozess (Franko, 1990; Kartschall et al., 1990).

Die Transformation der organischen Primärsubstanz C_POM(z,t) in aktive organische Substanz C_AOM(z,t) wird durch den Reaktionskoeffizienten k*₁ = k_syn · k_POM beschrieben, der als Produkt aus dem substratabhängigen Humussynthesekoeffizienten k_syn und dem Zersetzungskoeffizienten der POM berechnet wird. Der Übergang von Kohlenstoff in aktive organische Substanz wird bestimmt vom neu synthetisierten Anteil und der Menge, die zur Mineralisierung benötigt wird:

$\fn_jvn \frac{d}{dt}C_{AOM}(t)=k_{syn}\cdot k_{POM}\cdot R_{min}(t)\cdot C_{POM}(t)-k_{AOM}\cdot R_{min}(t)\cdot C_{AOM}(t)$

(57)

Wie viel Stickstoff in die aktive organische Substanz eingelagert wird, und wie viel mineralisiert wird, hängt vom C/N-Verhältnis der beiden organischen Fraktionen und dem Kohlenstoffbedarf der Humussynthese ab. Die Nettomineralisierung von Stickstoff aus der organischen Primärsubstanz ist analog zu Gl. (56). Der Stickstoffumsatz in der aktiven organischen Substanz verläuft ähnlich wie der Kohlenstoffumsatz, wobei das C/N-Verhältnis beider organischen Fraktionen Q_POM und Q_AOM den Synthesekoeffizient k_syn zu k^Q_syn modifiziert (Kartschall et al., 1990).

$\fn_jvn k_{syn}^{Q}=k_{syn}\cdot \frac{Q_{POM}}{Q_{AOM}}$

(58)

Außerdem wird die Veränderung des Ammonium- (N_NH4) und Nitrat-Stickstoffs (N_NO3) betrachtet. Somit wird der Stickstoff-Nettoumsatz durch das folgende System von Differentialgleichungen (Klöcking, 1991) für jede Bodenschicht beschrieben.

$\fn_jvn \frac{d}{dt}N_{POM}(t)=-k_{POM}\cdot R_{min}(t)\cdot N_{POM}(t)$

(59)

$\fn_jvn \frac{d}{dt}N_{AOM}(t)=k_{syn}^{Q}\cdot k_{POM}\cdot R_{min}(t)\cdot N_{POM}(t)-k_{AOM}\cdot R_{min}(t)\cdot N_{AOM}(t)$

(60)

$\fn_jvn \frac{d}{dt}N_{NH4}(t)=(1-k_{syn}^{Q})k_{POM}\cdot R_{min}(t)\cdot N_{POM}(t)+k_{AOM}(t)\cdot R_{min}(t\cdot N_{AOM}(t)-k_{nit}\cdot R_{nit}(t)\cdot N_{NH4}(t)$

(61)

(62)

Das Differentialgleichungssystem (59)-(62) mit den entsprechenden Anfangswerten wird mittels der Laplace-Transformation gelöst. Die optimalen Reaktionskoeffizienten dieser Prozesse können auf der Basis von Literaturangaben (s. Klöcking et al., 2007) durch Parameteroptimierung angepasst werden.

Analog zum Kohlenstoffumsatz erfolgt auch hier eine Reduktion der Mineralisierung und Nitrifizierung durch die Reduktionsfunktionen R_min(z,t) bzw. R_nit(z,t). Durch sie wird der Einfluss von Umweltbedingungen (Feuchte, Temperatur, pH-Wert) auf die Mineralisierung und die Nitrifizierung (Franko, 1990; Kartschall et al., 1990) beschrieben. Jede Einflusskomponente wird durch eine Einzelfunktion beschrieben, deren Produkt die gesamte Reduktionsfunktion ergibt:

$\fn_jvn R_{min/nit}=R_{min/nit}^{\Theta}(\Theta)\cdot R_{min/nit}^{BT}\cdot R_{min/nit}^{pH}(pH)$

(63)

R^θ_min/nit(θ) Feuchte-Reduktionsfunktionen der Mineralisierung bzw. der Nitrifizierung
R^BT_min/nit(BT) Bodentemperatur-Reduktionsfunktionen der Mineralisierung bzw. der Nitrifizierung
R^pH_min/nit(pH) pH-Wert-Reduktionsfunktionen der Mineralisierung bzw. der Nitrifizierung

Die Mineralisierung wird verzögert, wenn die Bodenfeuchte Werte von weniger als der Hälfte des Wassergehaltes bei Feldkapazität annimmt. Die Reduzierung der Nitrifizierung durch Trockenheit erfolgt ähnlich wie für die Mineralisierung, wobei jedoch auch eine Verminderung bei hohen Wassergehalten durch Sauerstoffmangel berücksichtigt wird (Abb. 7‑3).

Abb. 7‑3: Feuchte-Reduktionsfunktionen der Mineralisierung R^θ_min(θ) und der Nitrifizierung R^θ_nit(θ) in Abhängigkeit vom Verhältnis der aktuellen Bodenfeuchte zum Gesamtporenvolumen GPV

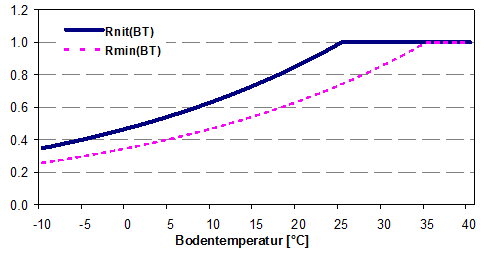
Der Einfluss der Bodentemperatur (BT) auf die Umsatzgeschwindigkeit wird nach Stanford et al. (1973) beschrieben. Dabei wird als optimale Temperatur für die Mineralisierung 35 °C und für die Nitrifizierung 25 °C angenommen (Abb. 7‑4).

Abb. 7‑4: Temperatur-Reduktionsfunktionen der Mineralisierung R^BT_min(BT) und der Nitrifizierung R^BT_nit(BT) in Abhängigkeit von der aktuellen Bodentemperatur BT

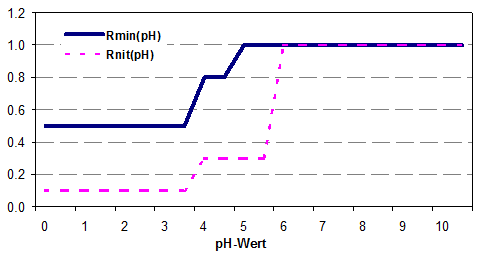
Außerdem werden Mineralisierung und Nitrifizierung durch ein saures Bodenmilieu gehemmt. Der Einfluss des pH-Wertes wird durch Stufenfunktionen (Abb. 7‑5) beschrieben. Der pH-Wert wirkt sich besonders stark auf die Nitrifizierung aus. Unterhalb eines pH-Wertes von 3 kommt die Nitrifizierung zum Erliegen. Optimale Nitrifizierungsbedingungen werden oberhalb eines pH-Wertes von 6 angenommen.

Abb. 7‑5: Säure-Reduktionsfunktionen der Mineralisierung und der Nitrifizierung in Abhängigkeit vom pH-Wert