Als Bodenkapillarwasser wird das Bodenwasser verstanden, das durch die Kapillarkräfte gegen die Schwerkraft gehalten werden kann, also der Feuchtegehalt bis Feldkapazität. Dieses Wasser kann nur durch Transpiration und Evaporation ausgeschöpft werden. Die Ausschöpfungstiefe bzw. die Mächtigkeit der wechselfeuchten Bodenzone wird dementsprechend durch die „Einflusstiefe“ der Vegetation (i.A. die Wurzeltiefe) und auf vegetationsfreien Standorten oder vegetationsfreien Perioden durch die „Einflusstiefe“ der Evaporation, also im Wesentlichen durch die Bodeneigenschaften (kapillare Saugspannung) bestimmt. Damit kann der Wassergehalt eines ungesättigten Standortes zwischen Feldkapazität FK und permanentem Welkepunkt PWP bzw. im Bereich des pflanzenverfügbaren Wassers (FK-PWP) schwanken. Die Speicherkapazität der wechselfeuchten Bodenzone HS ergibt sich damit zu (FK-PWP), bezogen auf die Mächtigkeit der verdunstungsbeeinflussten Bodenschicht (i.A. die Wurzeltiefe).
Innerhalb eines hydrologischen Modells besitzt die Modellierung des Bodenkapillarwasserhaushaltes dieser wechselfeuchten Bodenzone entscheidende Bedeutung, weil hier wichtige Abflussbildungsprozesse wie die Infiltration über die Feuchte und die Sickerwasserbildung gesteuert werden.
Eingangsgröße für die Modellierung des Bodenkapillarwasserhaushaltes ist der infiltrierende Niederschlagsanteil PB.
Da die flächenhaften Unterschiede der Bodenspeicherkapazitäten meist erheblich sind, sollten sie berücksichtigt werden, selbst bei der Betrachtung relativ kleiner, „homogen“ erscheinender Teilflächen. Dies lässt sich wie folgt begründen :
Im Boden sind allgemein bevorzugte Sickerwege vorhanden (Makroporen), längs derer einsickernde Niederschläge schneller in tiefere Bodenschichten gelangen können als bei völlig homogenen Bodenverhältnissen. Sobald das Bodenkapillarwasserdefizit in der Umgebung dieser Sickerwege aufgefüllt ist (sobald also der Bodenkapillarwasservorrat des gesamten Bodenprofils WSA größer ist als ein vorgegebener unterer Grenzwert HSMmin – der deutlich unter der mittleren Kapillarwasserspeicherkapazität der betrachteten Flächeneinheit liegen kann – kann bereits Sickerwasser PSO im Boden anfallen.
Die anfallende Sickerwassermenge PSO wird mit zunehmenden WSA kontinuierlich größer und sie kann (bei Annäherung von WSA an den teilflächenbezogenen Maximalwert HSMmax, vergl. Abbildung 2-4) die Größe des Gesamtwasserangebotes PB erreichen.
An dieser Stelle ist es notwendig, den Unterschied zwischen der auf einen Einzelstandort (ein Bodenprofil) bezogenen Speicherkapazität des Bodens für Kapillarwasser HSM (als profilbezogene Speicherhöhe) und dem entsprechenden, auf eine größere Fläche bezogenen Speichervorrat (-volumen) zu betrachten. Beide haben formal nur dann die gleiche Dimension (mm), wenn die Bezugsfläche gleich 1 gesetzt wird und alle Teilflächen in Bruchteilen von 1 und damit ebenfalls dimensionslos angegeben werden. Der zuvor erläuterte Unterschied muss unbedingt beachtet werden bei der Ermittlung dieser Modellparameter aus Standortkennwerten.
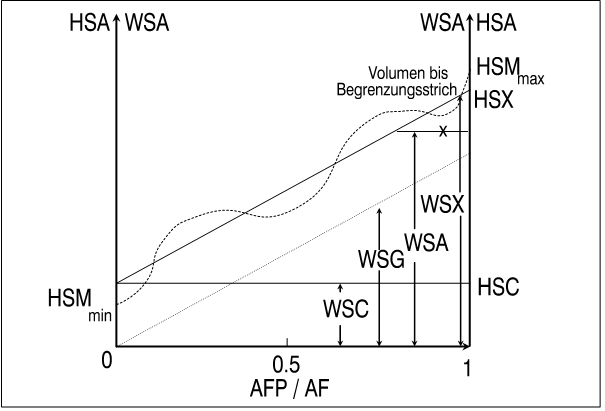
Nachfolgend wird die speichervolumenbezogene Betrachtung zugrunde gelegt (WSA usw.). Hierbei ergibt sich der Flächenanteil x von AF, auf dem noch freier Speicherraum für Bodenkapillarwasser vorhanden ist, aus dem aktuellen Bodenkapillarwasservorrat WSA der Fläche AF an Hand der generalisierten HSM-Linie in Abbildung 2-4 (jeweils als rechts von dieser Linie liegender Flächenanteil). Auf diesem Anteil trägt die gesamte Infiltration PB zur Auffüllung des Bodenkapillarwasservorrats bei, während sich auf dem restlichen Anteil (1-x) Sickerwasser bildet.
Abbildung 2-4: Reale und verallgemeinerte Verteilung der Bodenkapillarwasserspeicherkapazität
Solange WSA kleiner ist als WSC, wird die Infiltration auf der gesamten Fläche zu Bodenkapillarwasserrückhalt, d.h. sie trägt insgesamt zur Erhöhung der Bodenkapillarwasserspeichermenge WSA bei. Die momentane Auffüllungsintensität von WSA ist dann gleich der aktuellen Infiltrationsrate PB/DT (Flächenmittelwert der Infiltrationsrate, bezogen auf das Zeitintervall DT) :
Es sei erwähnt, dass sich diese Gleichung aus dWSA/dt = X * (PB/DT) Gl. 2-18 mit x=AFP/AF=1 ergibt. Durch Integration über DT erhält man den Gesamtfeuchtezuwachs DWSA=WSA-WSA1 (mit WSA1 als Speicherfüllung zu Beginn von DT) :
Ist WSA größer als WSC, so ist dWSA/dt= (PB/DT) Gl. 2-16 nur noch auf dem Anteil X der Fläche AF gültig, wo WSA noch kleiner als das lokale WSM ist (rechtes oberes Dreieck in Abbildung 2-4) :
Hier kann X durch WSA ausgedrückt werden :
Gl. 2-19
Durch Einsetzen von X in Gl. 2-18 ergibt sich
Hier repräsentiert D= (WSX-WSA) ein Bodenfeuchtedefizit, mit dem Gl. 2-20 umgeschrieben werden kann :
Unter der Annahme, dass während des Zeitschrittes DT PB = const. ist und das Defizit von D1 auf D abnimmt, wird folgende Lösung erhalten :
Der Bodenkapillarwasserrückhalt DWSA = D1-D = WSA-WSA1 ergibt sich danach mit D1 = (WSX-WSA1) zu :
Für WSA folgt daraus :
Die interessierende Bodensickerwasserbildung PSO der Teilfläche AF im Zeitintervall DT, die als Haupteingangsgröße der nachfolgenden Abflusskonzentrationsmodelle benötigt wird (hypodermischer Abfluss und Grundwasserabfluss), erhält man wie folgt :
Alle diese Gleichungen gelten für Zeitintervalle beliebiger Länge, sofern für sie in ausreichender Näherung PB = const. gesetzt werden kann. Diese Bedingung erfordert, dass beim Rechnen mit Zeitschritten größer als ein Tag eine Unterteilung des Zeitschrittes in mindestens zwei Teilzeitintervalle erfolgen muss (eine Niederschlagsperiode und eine niederschlagsfreie Periode).
Analoge Ansätze und Ableitungen ergeben sich für den Prozess der Bodenkapillarwasserausschöpfung durch Evapotranspiration in niederschlagsfreien oder -armen Perioden. Auf ihre Wiedergabe wird hier verzichtet, da die gleichen Arbeitsschritte wie oben vollzogen werden. Bemerkenswerte Unterschiede sind nur, dass die Eingangsgröße PB = PO (als Verdunstungsanspruch) negativ ist und auf Grund des bekannten Hystereseeffekts im Bodenfeuchteregime mit der in Abbildung 2-4 gepunktet eingetragenen Funktion gerechnet werden muss. Die resultierenden Berechnungsgleichungen lauten:
Wenn WSA größer als WSG ist, gilt gemäß DWSA= PB Gl. 2-17 :
Wenn WSA kleiner als WSG ist, gilt analog DWSA = (WSX-WSA1)*(1-exp(-PB/(WSX-WSC))) Gl. 2-24:
DWSA repräsentiert hier den aus dem Bodenkapillarwasservorrat ausgeschöpften Verdunstungsanteil der Fläche AF, wobei nach Gl. (2-25) WSA = WSA1+DWSA gilt. Aus Gl. (2-28) ergibt sich DWSA dem Betrag nach kleiner als PB, d.h. es entsteht eine Verdunstungsreduktion ED (als positive Größe), um die die reale Gebietsverdunstung zu reduzieren ist :
Die bisher diskutierten Überlegungen berücksichtigen flächenhafte Unterschiede der Speicherkapazität des Bodens für Kapillarwasser, nicht jedoch die vertikale Verteilung der jeweiligen aktuellen Speicherung. Dies entspricht teilweise nur sehr unzureichend den realen Verhältnissen, die dadurch gekennzeichnet sind, dass die Neuauffüllung des Bodens mit Wasser wie auch die Wiederausschöpfung stets von der Bodenoberfläche her erfolgt, d.h. zunächst immer die betrachtete Gesamtfläche betrifft. Ausgehend davon wurde ein Zweischichtkonzept entwickelt, nach welchem die Auffüllungs- und Ausschöpfungsberechnungen wie folgt ablaufen.
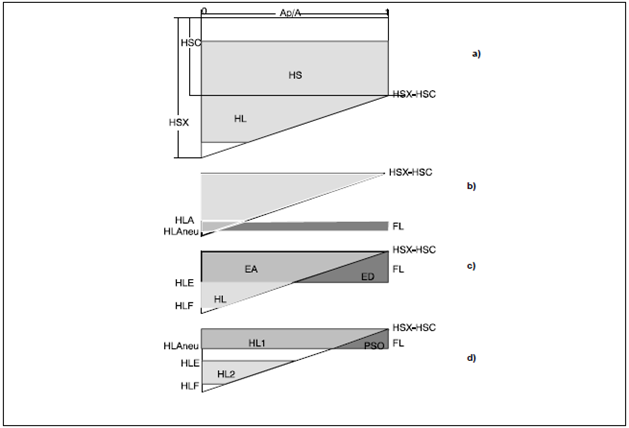
Es gibt einen oberen Speicher (erste Schicht) mit der Speicherkapazität HSC, während ein unterer Speicher (zweite Schicht) durch den Parameter HSX gekennzeichnet ist (Abbildung 2-4 und Abbildung 2-5a).
Die Speicherkapazität des unteren Speichers beträgt 0.5* (HSX-HSC) bzw. WSX-WSC. Auf diese Weise erfolgt die Berücksichtigung der flächenhaften Verteilung der Kapillarwasserspeicherkapazität.
Der obere Speicher ist gleichmäßig über die gesamte Bezugsfläche verteilt. In Niederschlagsperioden wird er bis HSC aufgefüllt. Weiteres ankommende Niederschlagswasser sickert in den unteren Speicher (Abbildung 2-5b).
Analog erfolgt in niederschlagsfreien bzw. -armen Perioden zunächst eine Ausschöpfung bis HS=0, erst dann beginnt die Ausschöpfung des unteren Speichers (Abbildung 2-5c). Ausschöpfung und Auffüllung des unteren Speichers finden also nur statt, wenn der Output des oberen Speichers ungleich Null ist, d.h. wenn die erste Schicht entweder völlig leer oder voll gefüllt ist. Damit wird berücksichtigt, dass alle Speicheränderungsprozesse von der Bodenoberfläche her erfolgen.
Im unteren Speicher werden maximal zwei Bodenkapillarwasserschichten betrachtet. Entsprechend dem genannten Grundsatz wird stets zuerst die obere Teilschicht ausgeschöpft bzw. aufgefüllt, danach die untere.
Zur Beschreibung der Lage dieser Teilschichten werden die Variablen HLA, HLE und HLF verwendet (Tabelle 2‑1, vgl. Abbildung 2-5).
Grundsätzlich gilt: HLA < HLE < HLF
Fall 1: ein Feuchteblock von 0 bis HLA „oben“
Fall 2: ein Feuchteblock von HLE bis HLF „schwebend“
Fall 3: zwei Feuchteblöcke, einer von 0 bis HLA „oben“, ein weiterer von HLE bis HLF „schwebend“
Wenn 2 Feuchteblöcke ausgebildet sind, und es tritt ein Ausschöpfungsintervall ein, so erfolgt zu Beginn desselben eine Zusammenlegung der beiden Teilschichten bei der mittleren Bezugsordinate. Diese Maßnahme, die den Berechnungsgang bemerkenswert vereinfacht, kann damit gerechtfertigt werden, dass das Gesamtvolumen des gespeicherten Bodenkapillarwassers nicht verändert wird und dass die Feuchteumlagerung folgenden zwei Umständen gerecht wird:
Abbildung 2-5: Prinzipskizzen zum Zweischichtkonzept
Tabelle 2‑1: Variablen zur Beschreibung des unteren Speichers
| Variable | zulässiger Bereich | mögliche Fälle | ||
| 1 | 2 | 3 | ||
| HLA | 0 bis HLE | 0 | 0 | > 0 |
| HLE | HLA bis HLF | 0 | > 0 | > 0 |
| HLF | 0 bis HSX-HSC | > 0 | > 0 | > 0 |
a) die Einsickerung erfolgt in bevorzugten Sickerbahnen, was dazu führt, dass unterhalb der ersten Schicht ein bestimmter Flächenanteil vom Sickerwasser schwerer erreicht wird;
b) tiefwurzelnde Pflanzen schöpfen auch aus größerer Tiefe Wasser, selbst wenn in höher gelegenen Schichten noch Wasservorräte vorhanden sind.
In nicht durch Ausschöpfungsintervalle unterbrochenen Auffüllungsperioden oder bei großem positiven Input wächst der Kapillarwasservorrat der zweiten Schicht zunächst von HLA bis HLE. Dann entsteht ein einheitlicher Feuchteblock von 0 bis HLA=HLF und HLA kann weiter ansteigen.
Der obere Speicher ist direkt durch Verdunstung ausschöpfbar. Kann der Bedarf durch den oberen Speicher nicht abgedeckt werden, kommt es zu einer Ausschöpfung des unteren Speichers. Hier findet allerdings eine Reduzierung der potentiellen Verdunstung um einen Anteil ED statt, der aus dem verfügbaren Bodenwasservorrat nicht abgedeckt werden kann.
Für ED gelten folgende Berechnungsformeln:
Gl. 2-30
Gl. 2-31
Die in Auffüllungsintervallen des unteren Speichers entstehende Sickerwassermenge PSO wird berechnet mit:
FL Output des oberen Speichers
HL Füllung des unteren Speichers am Ende des Berechnungszeitschrittes
Bei den bisherigen Ausführungen zum Bodenwasserhaushalt wurde immer davon ausgegangen, dass eine Auffüllung der Bodenfeuchte nur von „oben“, also letztlich durch den Niederschlag erfolgt. Auf grundwasserbeeinflussten bzw. -nahen Standorten kann allerdings auch eine Auffüllung der wechselfeuchten Bodenzone durch Kapillaraufstieg, also von „unten“ erfolgen. Für diesen Fall vereinfachen sich die bisher beschriebenen Modellalgorithmen. Als grundwassernah wird definitionsgemäß ein Standort oder eine Fläche dann bezeichnet, wenn der Grundwasserspiegel die wechselfeuchte Bodenzone erreicht oder innerhalb dieser liegt.
Diese wird durch den Ausschöpfungsbereich der Evapotranspiration bzw. die durchwurzelte Bodenzone begrenzt.
Für grundwassernahe Standorte wird ein auftretendes Bodenfeuchtedefizit durch den Kapillaraufstieg aufgefüllt, der als negative Grundwasserneubildung PSO nach Gl. (2-26) berechnet wird. Die reale Verdunstung ist gleich der potentiellen.
Das bedeutet letztlich, im stationären Zustand bzw. für als grundwassernah klassifizierte Flächen ist der Kapillaraufstieg gleich der potentiellen Verdunstung. Im instationären Zustand, wenn zeitlich veränderliche Grundwasserflurabstände berücksichtigt werden oder das Bodenwasserhaushaltsmodell mit einem Grundwassermodell gekoppelt ist, wird auch der Wechsel einer Fläche von grundwasserfern zu -nah und umgekehrt berücksichtigt. Erreicht der zeitlich variable Grundwasserstand den Bereich der Wurzelzone, wird das aktuelle Bodenfeuchtedefizit aufgefüllt.