Übersteigt das Wasserangebot an der Bodenoberfläche PO das aktuelle Infiltrations­vermögen Fpot des Bodens, so entsteht Ef­fek­tiv­nie­der­schlag PEF. Dabei gilt die Bilanzgleichung:

Der bodenwirksame Input PB (bzw. die aktuelle Infiltration) ergibt zu

Dieser Prozess kann mit Infiltrationsansätzen beschrieben werden.

Der Effektivniederschlag wird in einem Muldenspeicher der Kapazität WMM zwi­schen­ge­spei­chert und im nächsten Berech­nungszeitschritt erneut zur Infiltration angeboten. Beim Überlaufen dieses Speichers entsteht Landoberflächenabfluss. Die Kapazität dieses Speichers ist abhängig vom Geländege­fäl­le.

Bei ge­eig­neten Abflussbedingungen (merkliches Geländegefälle und „micro-channels“) und geringer Vorfluterentfernung der Entstehungsflächen erreicht dieser Landober­flächenabfluss schnell den Vorfluter und wird „abflusswirksam“. Er kann dann dem Di­rekt­abfluss RJ, also der schnellsten, meist ober­fläch­lich fließenden Abfluss­komponente in einem Einzugs­gebiet, zu­geordnet werden.

Die Infiltration spielt zusammen mit dem Bodenwasserhaushalt eine zentrale Rolle innerhalb des hydrologischen Regimes. Auf Grund der hohen Dynamik des Infiltrationsprozesses und seiner starken Abhän­gig­keit von sehr ortsvariablen Standorteigenschaften wie Bodenart (Leitfähigkeit, aber auch Porosität, Makropo­renanteil und Saug­span­nung) und zeitvariablen Einflüssen wie Bodenfeuchte und Be­ar­bei­tungszustand bei land­wirtschaftlichen Nutzflächen ist eine ex­akte Prozessbe­schreibung nur mit sehr detaillierten, standortbezo­genen Ansätzen hoher zeit­licher Auflösung (Minuten bis Stunden) möglich.

Diese Ansätze versagen in der Regel bei der Model­lie­rung größerer Flä­chen­einheiten, weil weder die notwendige ört­liche noch die zeitliche Auflösung der Ein­gangsdaten (Nieder­schlag), der System­zustände (Bodenfeuchte) und der System­eigen­schaf­ten (Bodenart) ge­geben ist.

Es wurden deshalb Ansätze ent­wickelt, die für größere Zeit- und Raum-Di­men­sionen den Ef­fek­tiv­niederschlag als Ziel­grö­ße rich­tig berech­nen, wobei toleriert wurde, dass Teilpro­zesse wie das Fortschreiten der Feuch­tefront im Boden ver­nachlässigt werden.

Unter der Voraussetzung, dass der „zeit­liche Verlauf von Infiltra­tions­vermögen und -inten­sität in be­friedigender Weise als Funk­tion des im Boden gespeicherten Was­sers berechnet werden kann“ (Peschke 1980), wurde das Kon­zept INFILT zur Modellierung des In­fil­trationsprozesses ent­wickelt. Es berücksichtigt ver­ein­facht linear die flächenhafte Ver­teilung der gesättigten hy­drau­lischen Leitfähigkeit in­ner­halb der jeweiligen Bezugsfläche.

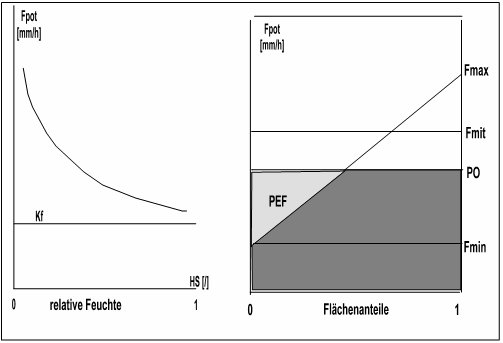
Der Vorteil die­ser Vorgehensweise wird in Abbildung 2-3 (rechts) ver­deut­licht. Wäh­rend Ansätze, die nur das mitt­lere Infiltrationsvermögen Fmit be­trach­ten, im angegebe­nen Fall keinen Effektivnieder­schlag be­rech­nen, ermittelt INFILT für Standorte mit geringem Infiltrations­ver­mö­gen einen Effektiv­niederschlag PEF (hellgraues Dreieck).

Abbildung 2-3: Das Infiltrationsvermögen F als Flächenfunktion (rechts) und die Infiltrationsintensität in Abhängigkeit von der Boden­feuchte (links)

Ausgegangen wurde bei der Ableitung der Berechnungsgleichung für das aktuelle Infiltrationsvermögen Fpot eines Standortes von der Infil­trationsgleichung nach HOLTAN:

mit

Fv – Infiltrationsintensität
Fc – stationärer Endwert von Fv
BD – Bodenfeuchtedefizit
A,n – empirische Parameter (zit. bei Peschke 1980)

Mit n=2, Fc=K_f*DT und Fv=Fpot ergibt sich Fpot=A*(HS-1)²+K_f*DT. Unter der Annahme, dass der empirische Parameter A von der gesät­tigten hydraulischen Leitfähigkeit K_f abhängt, lässt sich diese Gleichung mit A=EXH*Kf*DT leicht überführen in

mit EXH als empirischer Parameter und BD=(HS-HSC)/HSC als Füllungsdefizit des Bodenkapillarwasser­spei­chers des Oberbodens.

Das Infiltrationsvermögen Fpot ist also bestimmt durch die gesät­tigte hydraulische Leit­fä­hig­keit und die aktuelle Boden­feuch­te. „Die suk­zessive Auf­feuch­tung bei fortschreitender In­fil­tration re­duziert … die In­filtrationsintensität Fpot. Er­reicht sie schließ­lich ver­nach­läs­sigbar kleine Werte (also Sät­ti­gung und da­mit HS = 1, vgl. Abbildung 2-3, links), stellt sich Fpot auf den konstanten Wert der gesät­tigten hydrau­lischen Leit­fähigkeit in der Oberfläche ein. Für die hohen Infil­tra­tions­in­ten­sitäten im Anfangs­stadium der Infiltration sind also die Adsorp­tions- und Kapillarkräfte erforderlich, wäh­rend der Pro­zess im Spätstadium mit gerin­gen Intensitäten durch die Schwer­kraft … auf­rechterhalten wird.“ (Dyck/Peschke 1983)

Für das Minimum GLN und das Maximum GLX der linearisierten Verteilung der K_f-Werte einer Fläche wird nach Fv = A*BDn + Fc Gl. 2-11 je­weils Fmin und Fmax errechnet, wo­mit sich dann das auf die Fläche bezogene, potenti­elle Infiltrationsvermögen FPOT ermitteln lässt zu :

 für 

 für 

 für 

wobei mit FPOT=MAX(0.,FPOT) ein positiver Wert für FPOT zu sichern ist. Die Modell­ausgänge berechnen sich nun zu

und PB als Infiltration bzw. Modelleingang für das Bodenwasser­haus­haltsmodell zu

Der beschriebene Ansatz wird in Kombination mit einen einfachen Ansatz zur Berücksichtigung der Muldenspeicherung (analog der Interzeptionsspeicherung) abgearbeitet. Der berechnete Effektivniederschlag PEF bildet den Input in diesen Speicher, dessen Überlauf abflusswirksam wird und eine Komponente des Landoberflächenabfluss RO bildet. Zu Beginn jeden Berechnungszeitschritts wird der aktuelle Inhalt des Muldenspeichers gemeinsam mit dem Output des Inter­zeptions­speichers PO zur Infiltration angeboten. Beide Ansätze können auf beliebige, heterogene Flächen ange­wendet werden, um die Auf­tei­lung des bodenwirksamen Nie­derschlages in Ef­fek­tiv­niederschlag bzw. Landoberflächenabfluss und Einsicke­rung in den Boden PB zu be­rech­nen. PB wiederum bildet den Input für das nachfolgend beschriebene Bodenwasserhaushaltsmodell.

/* Bei Bodenfrost wird davon ausgegangen, dass ein feuchteres Gebiet geringer durchlaessig als ein trockenes ist */
/* Anwendung für grundwasserferne Flaeche */

if( !gw_nah ) {
if(bod_waerme < 0.)  {
if(hsc > 0.)  {
tt   = *FrostFaktor() * (hs / hsc);
*aimpn = MIN(1., tt + *aimpn);
// PrintTest(1,“bodenw=%f hs/hsc=%f tt=%f
aimpn=%f\n“,bod_waerme,*hs/ *hsc,tt,aimpn);
}
}
}
Ermittlung der Bodenwärme
if(*ss3 < 0.)
*ss3 = *ss3;

if(ss1 < 5.)  {  /* Bodenwaerme aendert sich nur, wenn keine oder eine geringe Schneedecke vorhanden ist */
if( bt > 0.)  {
*ss3 += bt;
if(*ss3 > 0.)
*ss3 = 0.;
}
else  {
if(*ss3 < 0.)
*ss3 += bt;
else
*ss3 = bt;
}
}